Die Logistische Regression ist ein statistisches Verfahren, um binäre Ereignisse zu schätzen. Dabei werden ähnlich wie bei der Linearen Regression beliebig viele unabhängige Variablen (X) verwendet, um eine abhängige binäre Variable Y (mit den Ausprägungen 0 und 1) zu berechnen. Genauer gesagt, versucht man mit Hilfe der logistischen Regression den Einfluss von X auf Y zu schätzen. Für jeden Regressor werden, i.d.R. mithilfe einer Maximum-Likelihood-Schätzung, Koeffizienten βi geschätzt. Die Koeffizienten geben Einflussstärke (Höhe des Koeffizienten) und Einflussrichtung (Vorzeichen des Koeffizienten) an.
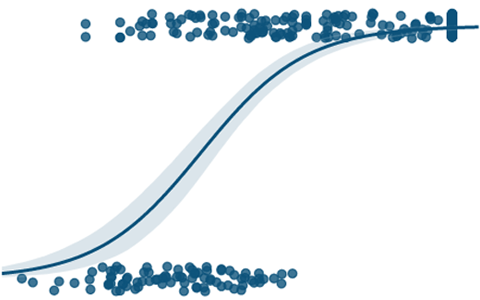
Oftmals verläuft die Kurve der logistischen Regression wie ein S. Auf der Y-Achse ist die Wahrscheinlichkeit abgetragen, wohingegen die X-Achse eine bestimmte Regressor-Variable widerspiegelt.
Interpretation der Regressionskoeffizienten
Durch notwendige mathematische Umformungen werden die Koeffizienten transformiert. Dadurch sind sie in ihrer Einflussstärke nicht mehr direkt interpretierbar – im Gegensatz zur Linearen Regression. Oftmals werden daher die sogenannten „Odds-Ratios“ gebildet, da diese eine einfachere Interpretation ermöglichen. Die Odds-Ratios beschreiben die Veränderung des Wahrscheinlichkeitsverhältnisses. Dieses ist jedoch nicht gleichzusetzen mit der Veränderung der absoluten Wahrscheinlichkeit!
Blogbeiträge zur Interpretation der Koeffizienten oder Umsetzung einer Logistischen Regression finden sich hier:
Abschließend empfiehlt sich, bei der Interpretation ein größeres Augenmerk auf die Einflussrichtung statt der Einflussstärke zu legen.
Anwendungsfall - Eine Logistische Regression
Die Anwendung von logistischen Regression ist vielfältig und auf zahlreiche Business-Kontexte übertragbar. Ob Vorhersage der Kündigung von Kunden oder Mitarbeitern bis hin zur Berechnung von Response-Wahrscheinlichkeiten für Vertriebsaktionen. Übertragen auf den Vertriebskontext könnte dies bedeuten: Die logistische Regression schätzt, ob Kunden ein Produkt abschließen oder nicht (Zielvariable Y). Als Regressoren (X) können beispielsweise das Alter, die Anzahl der Logins, das Geschlecht und ein Kundenscore (bspw. Häufigkeit der Käufe und Höhe der Käufe) benutzt werden.
Regressionsgleichung
Abschlusswahrscheinlichkeit (0 oder 1) = β0 + β1*Alter + β2*Anzahl Logins + β3*Geschlecht + β4*Kundenscore
Bei obigem Beispiel ließe sich vermuten, dass die Anzahl der Logins und der Kundenscore einen positiven Einfluss auf die Wahrscheinlichkeit des Abschlusses haben. Je aktiver (Anzahl Logins) ein Kunde, desto höher tendenziell sein Interesse an den jeweiligen Produkten. Je umsatzstärker ein Kunde (Kundenscore), desto höher tendenziell die Bereitschaft weitere Produkte zu kaufen (Cross-Selling). Dies ließe sich mithilfe der Logistischen Regression verifizieren (zumindest auf korrelativer Ebene).
Die logistische Regression zählt im Machine Learning zu den Supervised Learning Verfahren, da die Zielvariable (Y) bekannt ist. Allein die logistische Regression hat noch keine Machine Learning Charakteristika. Diese kommen hinzu, wenn verschiedene Modelle gegeneinander getestet werden und kontinuierlich mit neuen Daten aktualisiert werden. So „lernt“ das Modell.
Code Snippet
from sklearn.linear_model import LogisticRegression
reg = LogisticRegression().fit(X_train, y_train)
reg.coef
Der Code Snippet ist in der Programmiersprache Python geschrieben und basiert auf dem Modul scikit-learn.
Weiterführende Ressourcen zu Machine Learning
Datenintegration
Wie Machine Learning von Datenintegration profitiert
Die Kausalkette „Datenintegration-Datenqualität-Modellperformance“ beschreibt die Notwendigkeit von effektiver Datenintegration für einfacher und schneller umsetzbares sowie erfolgreicheres Machine Learning. Kurzum: aus guter Datenintegration folgt bessere Vorhersagekraft der Machine Learning Modelle wegen höherer Datenqualität.
Betriebswirtschaftlich liegen sowohl kostensenkende als auch umsatzsteigernde Einflüsse vor. Kostensenkend ist die Entwicklung der Modelle (weniger Custom Code, damit weniger Wartung etc.). Umsatzsteigernd ist die bessere Vorhersagekraft der Modelle, was präziseres Targeting, Cross- und Upselling und ein genaueres Bewerten von Leads und Opportunities betrifft – sowohl im B2B- als auch im B2C-Bereich. Hier findest du einen detaillierten Artikel zu dem Thema:
Plattform
Wie du Machine Learning mit der Integration Platform verwendest
Du kannst die Daten deiner zentralen Marini Integration Platform externen Machine Learning Services und Applikationen zur Verfügung stellen. Die Anbindung funktioniert nahtlos durch die HubEngine oder direkten Zugang zur Plattform, abhängig von den Anforderungen des Drittanbieters. Ein Anbieter für Standardanwendungen des Machine Learnings im Vertrieb ist z.B. Omikron. Du kannst aber auch Standardanwendungen auf AWS oder in der Google Cloud nutzen. Eine Anbindung an deine eigenen Server ist ebenso problemlos möglich, wenn du dort deine eigenen Modelle programmieren möchtest.
Wenn du Unterstützung dabei brauchst, wie du Machine Learning Modelle in deine Plattform einbinden kannst, dann kontaktiere unseren Vertrieb. Wir helfen dir gerne weiter!
Anwendungsbeispiele
Häufige Anwendungsszenarien von Machine Learning im Vertrieb
Machine Learning kann auf vielfältige Weise den Vertrieb unterstützen. Es können zum Beispiel Abschlusswahrscheinlichkeiten berechnet, Cross- und Up-Selling-Potenziale geschätzt oder Empfehlungen vorhergesagt werden. Wichtig dabei ist, dass der Vertriebler unterstützt wird und eine weitere Entscheidungshilfe erhält, anhand derer er sich besser auf seine eigentliche Tätigkeit, nämlich das Verkaufen, konzentrieren kann. So kann der Vertriebler zum Beispiel schneller erkennen, welche Leads, Opportunities oder Kunden am vielversprechendsten momentan sind und diese kontaktieren. Es bleibt jedoch klar, dass der Vertriebler die letztendliche Entscheidung trifft und durch das Machine Learning letztlich nur Erleichterungen erfährt. Schlussendlich verkauft kein Modell, sondern immer noch der Mensch.
Hier findest du eine kurze Einführung in das Thema Machine Learning und die häufigsten Anwendungsmöglichkeiten im Vertrieb.