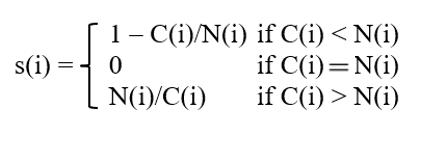Clusteranalyse

Die Clusteranalyse zählt im Machine Learning zur Kategorie des Unsupervised Learnings. Ziel ist es, k Cluster zu generieren. Die Cluster sollten untereinander maximal heterogen und innerhalb maximal homogen sein. Clusteranalysen werden beispielsweise häufig verwendet, um Kunden zu segmentieren und somit gezielter anzusprechen zu können (Targeting). Die nachfolgenden Darstellungen basieren auf realen Kundendaten und sollen beispielhaft die wichtigsten Konzepte der Clusteranalyse verdeutlichen.

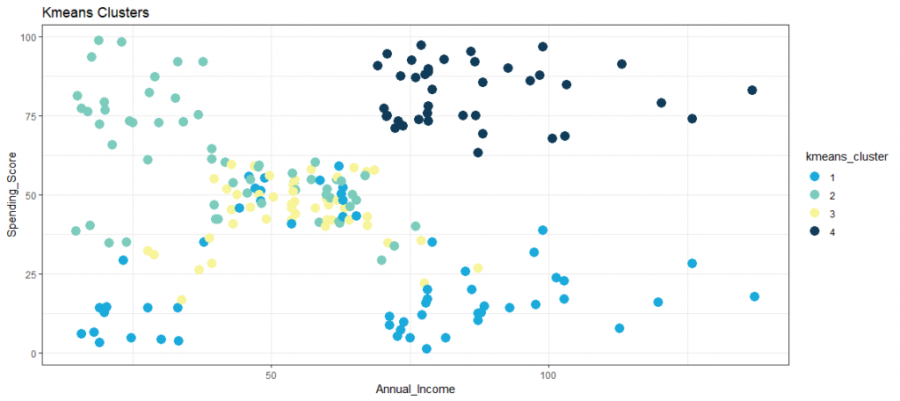
Eine sehr beliebte und etablierte Clustering-Methode ist der k-Means- Algorithmus, der n Beobachtungen in k-Cluster durch iteratives Minimieren der Abstände innerhalb eines Clusters und maximieren der Abstände zwischen den Clustern teilt. Zuerst werden zufällige Zentroide der Anzahl k in das multidimensionale Koordinatensystem gesetzt. In einem zweiten Schritt werden die Abstände jeder Beobachtung zu jedem Schwerpunkt berechnet, dann werden die Beobachtungen dem Zentroid (Cluster) zugeordnet, dem sie am nächsten sind. In einem dritten Schritt werden die Zentroide in der Mitte des Clusters platziert. Nun werden die Schritte eins bis drei wiederholt, bis es keine weitere Neuzuordnung von Beobachtungen zu Clustern gibt. Die Anzahl der Cluster k und damit die anfänglichen Zentroide müssen a priori definiert werden. Die Abbildung zeigt eine beispielhafte Visualisierung eines k-Means-Verfahren mit k = 4 Clustern.

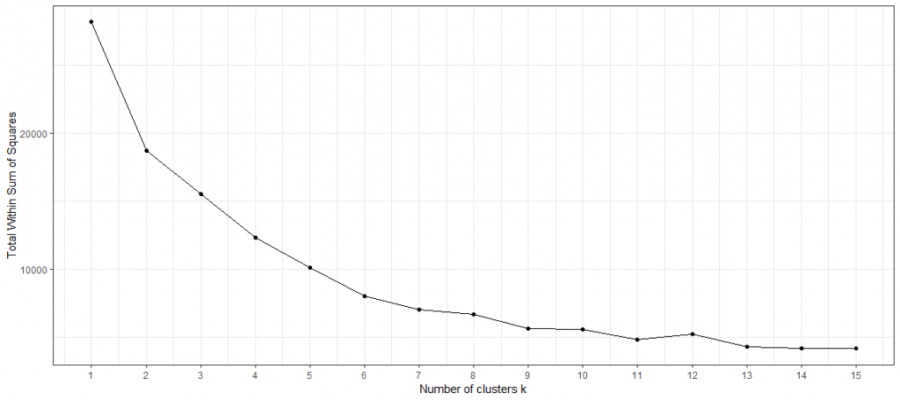
Dies wirft die erste Frage auf: Wie wählt man die richtige Anzahl von Clustern aus? Eine mögliche Methode dafür könnte das Ellenbogendiagramm sein. Es bildet die Varianz gegen die Anzahl der Cluster ab. Bei der k-Means- Methode hat jeder Cluster einen Zentroiden, der sein „Zentrum“ bestimmt. Total-Within-Clusters-Sum-Of-Squares (TWSS) ist die Summe der quadrierten Abstände jeder Beobachtung von ihrem Zentroiden. Je kleiner die Quadratsumme, desto geringer der Abstand, desto höher die Ähnlichkeit. Ein niedriger TWSS-Wert zeigt an, dass die Beobachtungen in der Nähe ihrer Zentroide liegen.

Im Gegensatz dazu würde eine hohe TWSS darauf hindeuten, dass die Abstände zwischen den Beobachtungen und ihren Zentroiden hoch sind, was vermuten ließe, dass die Beobachtungen nicht gut zu ihren jeweiligen Cluster verteilt sind. Abschließend gibt die TWSS eine Metrik an, um zu bewerten, wie gut die Beobachtungen gebündelt sind. Da die TWSS mit jedem zusätzlichen Cluster per Definition abnimmt, gibt es einen Trade-Off zwischen TWSS und der Anzahl der Cluster. Durch die Darstellung der TWSS und der Anzahl der Cluster ist es möglich, heuristisch die Anzahl der Cluster durch Inferenz des Auges zu bestimmen.

Der Name ergibt sich aus der oft gesehenen ellenbogenartigen Form des Liniendiagramms. Die optimale Anzahl der Cluster basierend auf dem Ellbogendiagramm ist nicht immer eindeutig. Generell gilt: Wähle das k, an dem das Liniendiagramm einen Knick (wie bei einem Ellenbogen) aufweist. Hier flacht die Steigung ab und somit ebenso die Abnahme der TWSS. Das obige Ellenbogendiagramm lässt heuristisch keine optimale Anzahl an Clustern erkennen. Daher muss eine andere Metrik zur Bestimmung herangezogen werden.

Ist beim Ellenbogendiagramm kein Knick auszumachen, kann der Silhouettenkoeffizient herangezogen werden. Er berechnet sich folgendermaßen:

wobei:

• C(i) = Distanz zu eigenem Cluster von Beobachtung i
• N(i) = Distanz zu nächstem Nachbarn von anderem Cluster von Beobachtung i

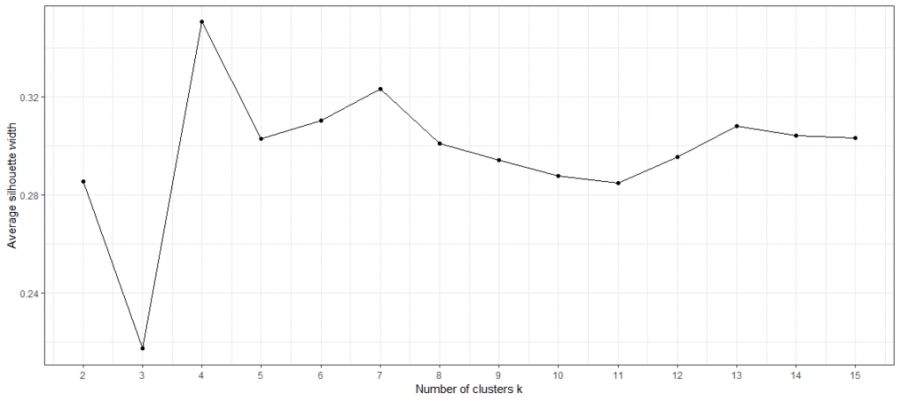
Der Silhouettenkoeffizient reicht von 1 bis -1, wobei 1 anzeigt, dass die Beobachtung gut zu ihrem aktuellen Cluster passt, 0, dass sie sich am Rand von zwei Clustern befindet und -1, dass sie besser zu einem anderen Cluster passt. Nach der Berechnung des Silhouettenkoeffizienten für jede einzelne Beobachtung kann der durchschnittliche Silhouettenkoeffizient berechnet werden und als Gesamtindikator dafür verwendet werden, wie gut Beobachtungen zu ihren jeweiligen Cluster passen. Je höher der durchschnittliche Silhouettenkoeffizient, desto besser passt jede Beobachtung im Durchschnitt zu ihren Cluster. Auf der unteren Abbildung des durchschnittlichen Silhouettenkoeffizienten ist die optimale Anzahl an Clustern deutlich erkennbar mit k = 4.

Der HC-Algorithmus arbeitet anders als der k-Means-Ansatz. Beide verfolgen einen iterativen Ansatz. Im ersten Schritt von HC bilden die am nächsten beieinander liegenden Beobachtungen (teilen den kleinsten Abstand) eine Menge. In Schritt zwei wird der Abstand zwischen allen anderen Beobachtungen zueinander und zur Menge aus Schritt eins betrachtet. Auch hier wird der niedrigste Abstand gewählt. Teilen zwei Beobachtungen den kleinsten Abstand, bilden sie eine neue Menge. Wenn der kleinste Abstand zwischen einer Beobachtung und einer Menge geteilt wird, wird die Beobachtung zu der Menge hinzugefügt. Wenn nur noch Mengen übrig sind, wird der Abstand zwischen den Mengen berücksichtigt und die Mengen zusammengefasst. Dieser Vorgang wiederholt sich, bis es nur noch ein endgültiges Cluster gibt. So wird eine hierarchische Struktur aufgebaut.

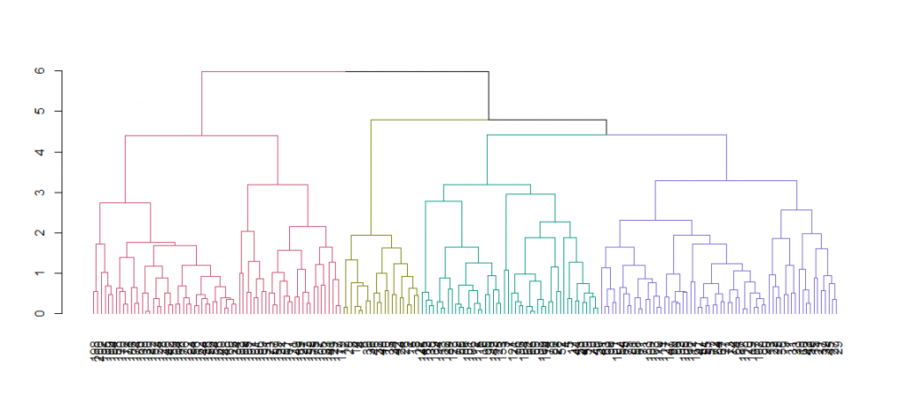
Visualisierung von Hierarchical Clustering

Der Abstand zwischen den Beobachtungen/Clustern wird beispielsweise durch das „complete linkage“-Kriterium bestimmt. Im Gegensatz zum k-Means-Algorithmus ist die Anzahl der Cluster nicht a priori, sondern posterior definiert. Durch den iterativen Ansatz, Beobachtungen iterativ Mengen zuzuordnen, kann das Ergebnis in einem Dendrogramm visualisiert werden.

Ein hands-on Tutorial in Python, findest du in diesem Blogbeitrag auf TowardsDataScience.